卡扣设计的原则

卡扣设计的最终目标是要实现两个零件之间的成功连接固定，要达到连接固定的效果，卡扣设计时需要从以下几方面进行考虑：连接可靠性、约束完整性和装配协调性，它们是卡扣连接成功的关键要求，其他要求还应该包括制造工艺的可行性、成本的高低等。

连接可靠性，是卡扣设计中最重要的一个设计指标，一般会从以下几个方面去考虑：

l 连接符合功能预期；

l 连接强度；

l 在用户使用过程中不发生分离、松动、破损、噪声；

l 能够适应使用过程中因环境因素引起的产品变形或蠕变；

l 保证维修拆卸的功能与设计预期一致。

实际上，在产品设计过程中，会根据产品的定位、部件的功能以及成本去选择需要满足的连接可靠性要求，并不是每个设计都需要完全满足以上要求，比如有些设计不需要经常拆卸或维修，那么设计符合前三点就可以，如果需要经常拆卸，那么就需要考虑拆后卡扣的功能与设计预期一致，此时卡扣设计的类型选择或具体设计参数上就会有所改变，比如下图中同样是电池盖，但是应用在充电宝和遥控器上卡扣的设计就会不同。

下面针对悬臂梁卡扣的连接强度计算进行分析介绍：

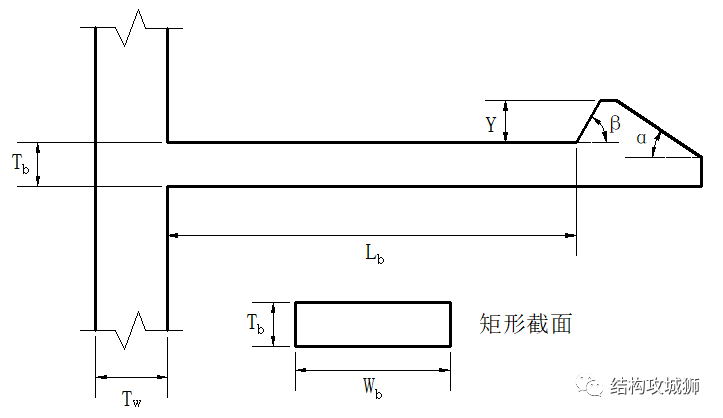
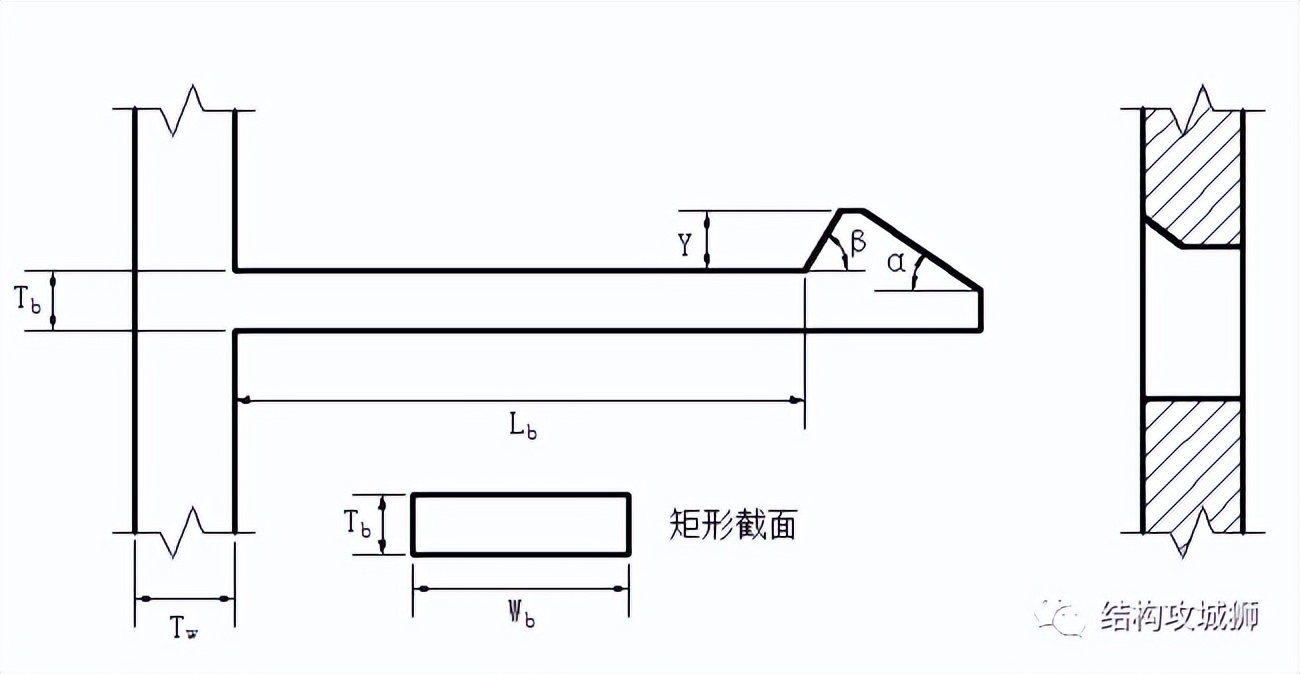
一、常见的悬臂梁卡扣的主要有以下参数：

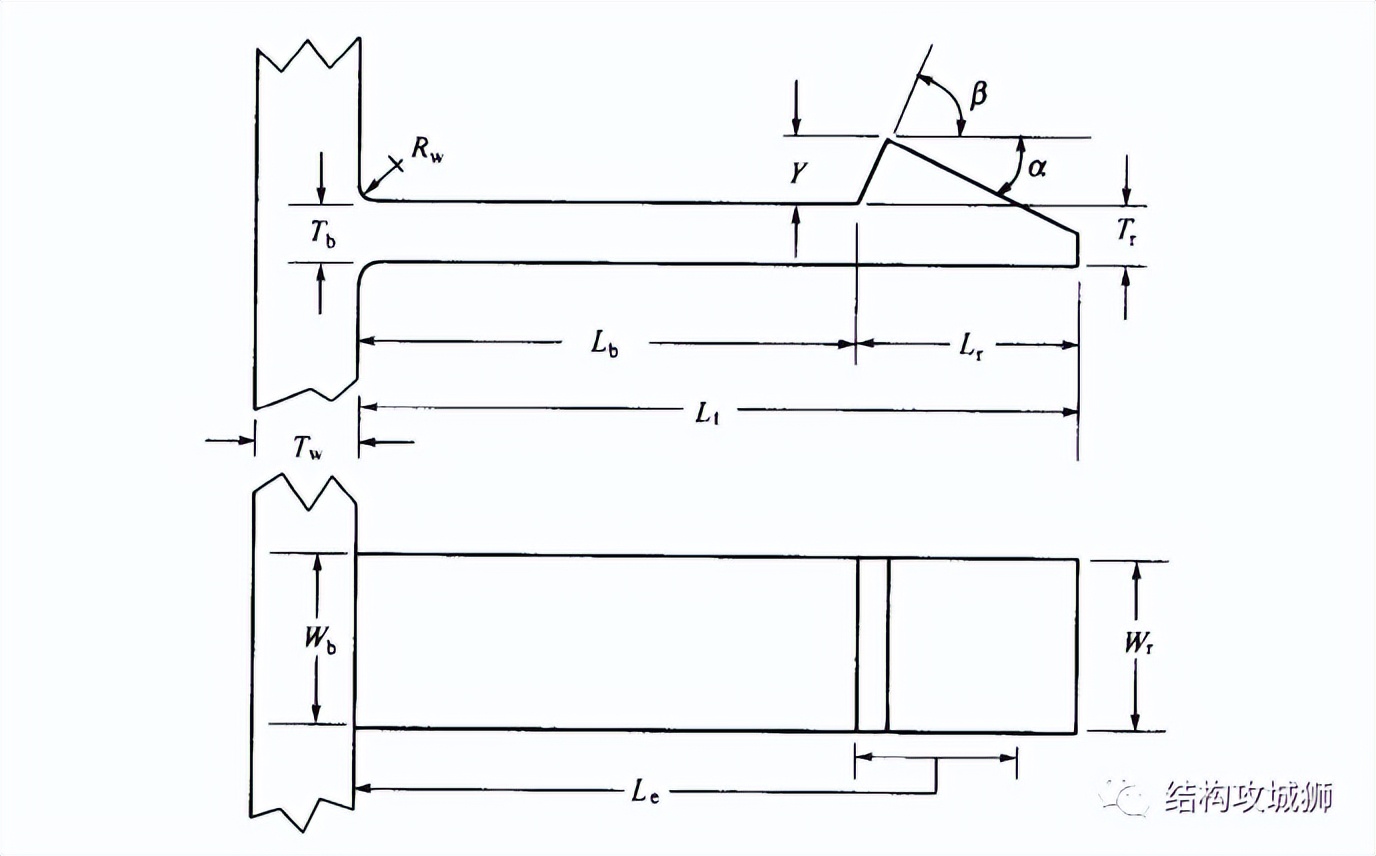
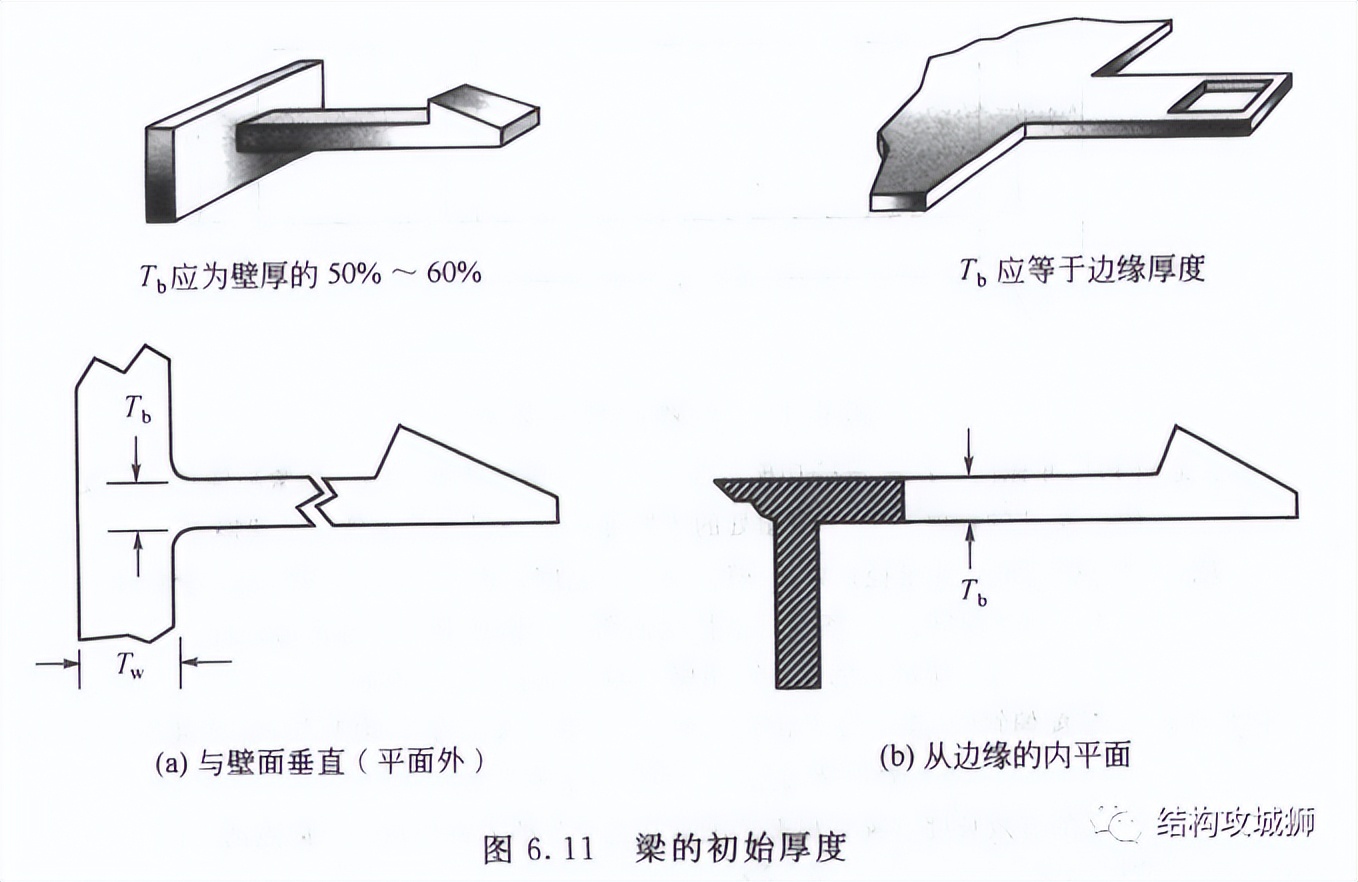
1、梁根部的厚度Tb

Tb一般为壁厚Tw的50%~60%，太小可能会存在充模和流动问题，太大可能会存在冷却问题，进而会导致大的残余应力、缩孔和缩痕。当梁是从壁面延伸出来时，Tb可等于Tw。

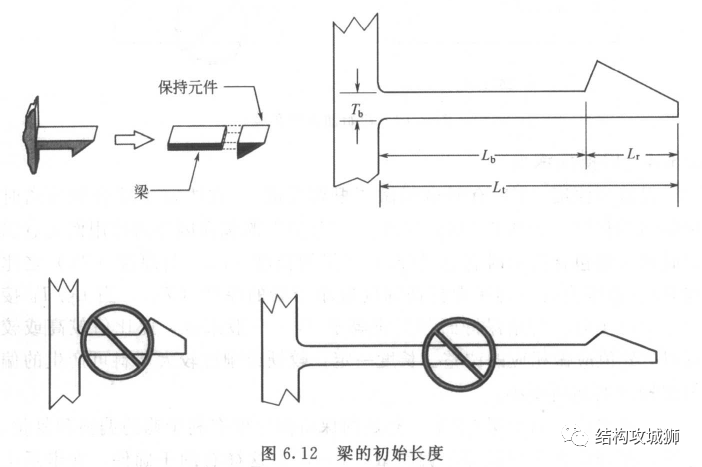
2、梁的长度Lb

悬臂梁卡扣的总长（Lt）由梁的长度（Lb）和保持元件长度（Lr）组成，Lb取值范围一般为5Tb~10Tb，大于10Tb时，可能会存在翘曲和充填问题，小于5Tb时，梁的柔性较差，梁的根部承受较大的弯曲，从而增大损坏的可能性。（对于较硬或较脆的塑料，应采用较大的长度与厚度的比值）。

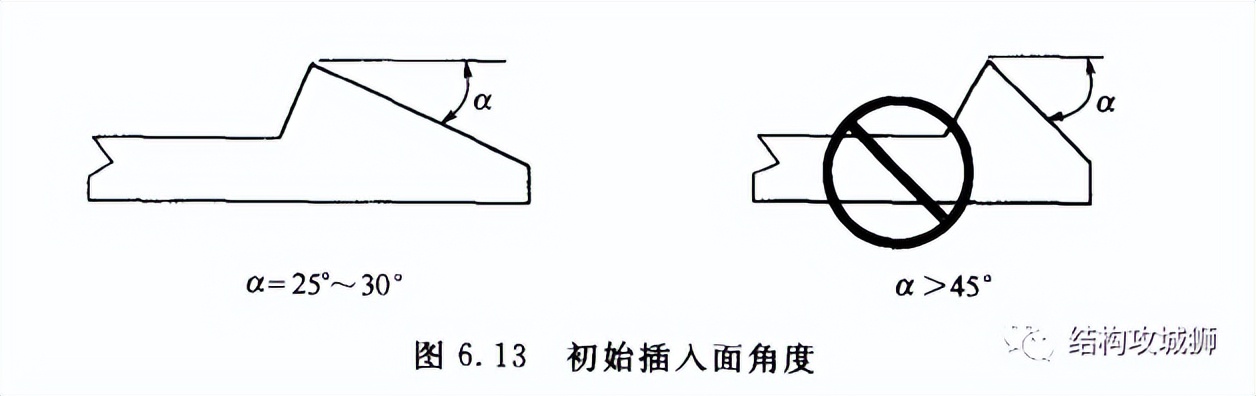
3、插入面角度α

插入面角度会影响装配力，角度越大，装配力就越大，一般合理的角度在25°~35°之间，如果因空间问题（即α越小，保持元件的长度Lr越长），最大不要超过45°。

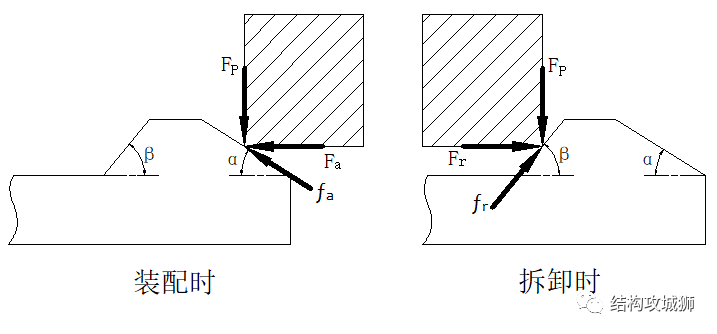
4、保持面角度β

保持面角度会影响保持强度和分离力，角度越大，保持强度和分离力就越大，保持面角度β应根据拆卸情况而定：

l β≈35°，用于不需要外部分离力的可拆卸锁紧件；

l β≈45°，用于需小的外部分离力的可拆卸锁紧件；

l β≈80°~90°，用于需很大外部分离力的非拆卸锁紧件；

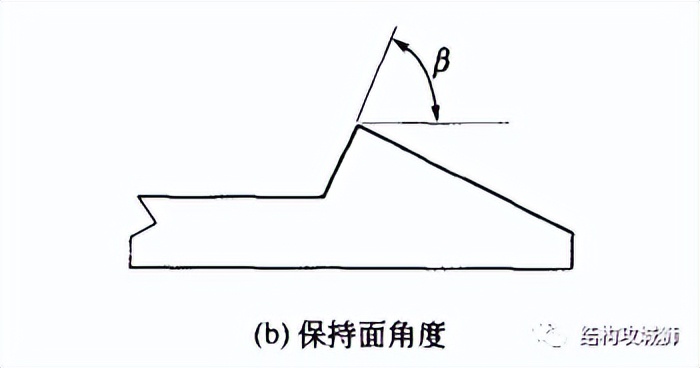
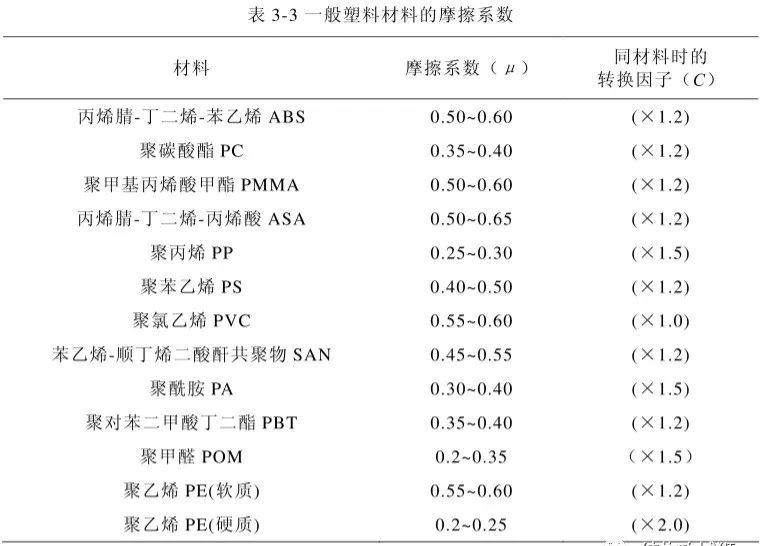
如果，卡扣需要有足够的保持强度，保持面角度可在极限角度与90之间取一个角度值，（由于接触面之间存在摩擦，接近90°的保持面角度仍然与90°角起到的作用是一样的）。根据基本保持力方程，极限角：

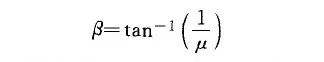
由此可见，摩擦系数越大，极限角度越小，但考虑到注塑成型后的影响，一般选择接近90°，保持面角度选择在80°~90°之间还有下图好处：

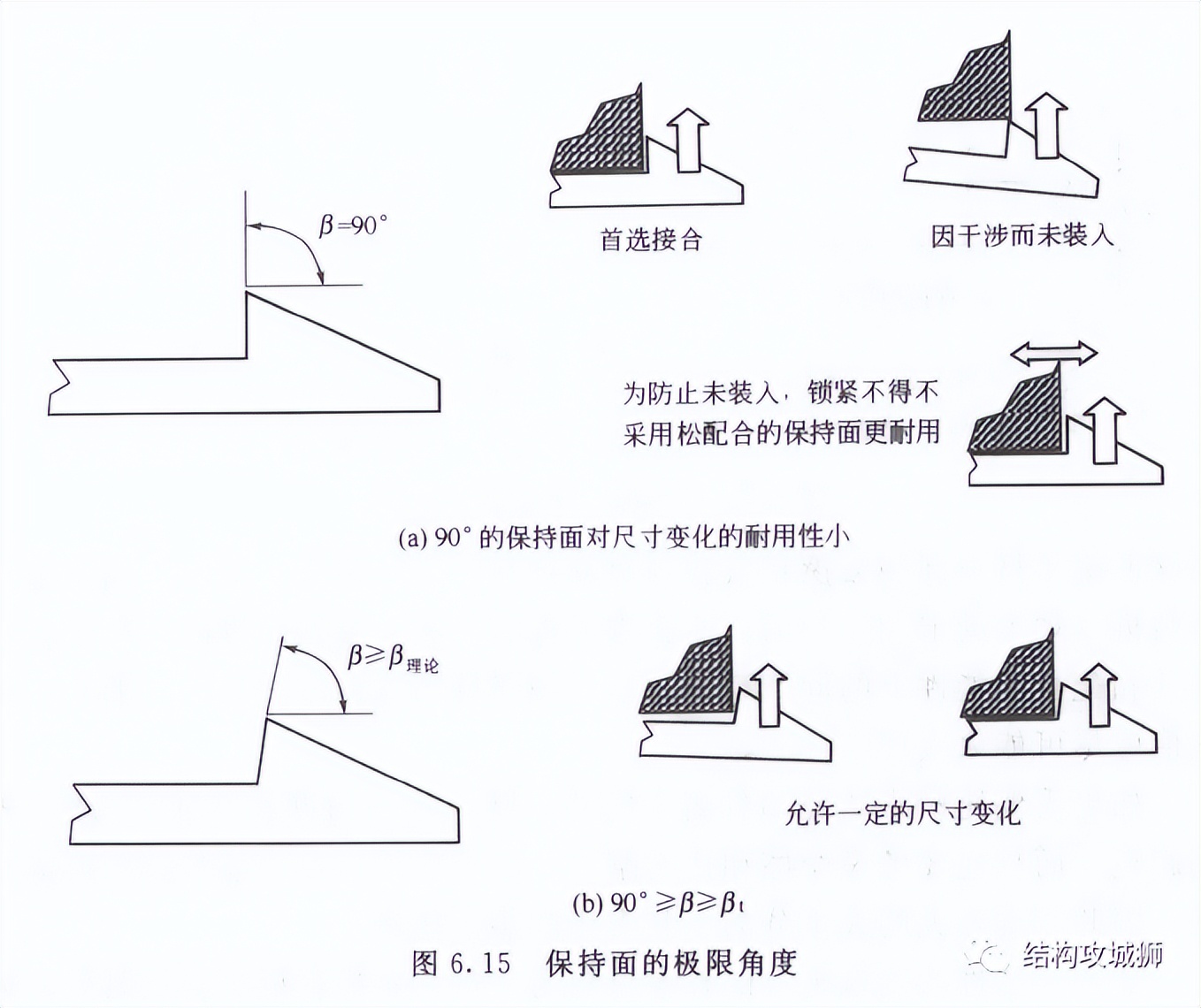
5、保持面深度Y

它决定了接合和分离时梁偏斜的程度，一般情况下，

l 当Lb/Tb≈5时，Y<Tb；

l 当Lb/Tb≈10时，Y=Tb；

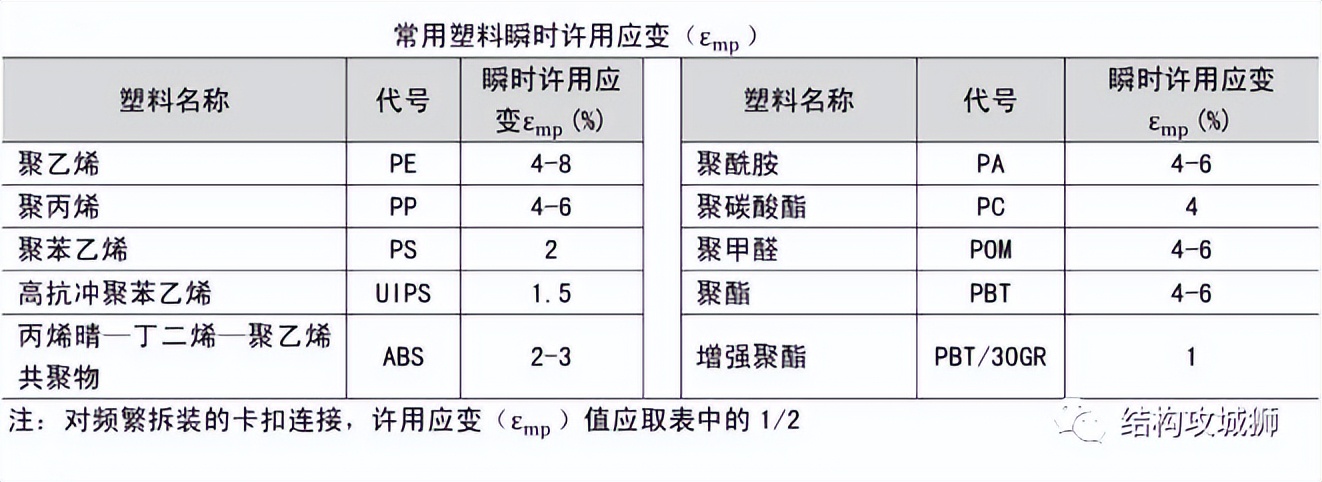
l 当Lb/Tb较大或较小时，Y值应做相应调整，同时，对于较硬或刚性较大的塑胶，Y值相应取小些。（保持面最大深度应≤材料最大许用应变）

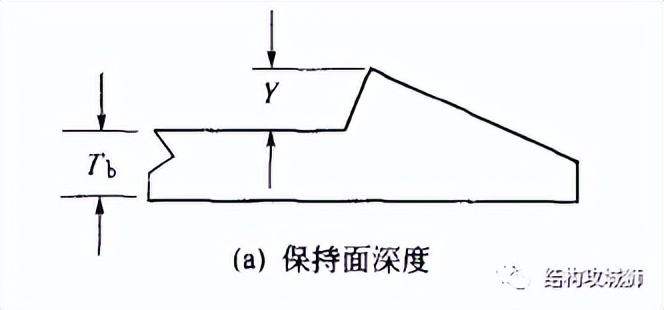
还有，保持面深度应尽量接近等于偏斜量（Y=δ），这样卡扣上的分离力会尽可能接近梁的中性轴，保持强度得到提高。

6、保持元件处的梁厚度Tr

一般情况下，Tr常常接近梁根部的厚度Tb（为了出模，只是有很小的出模斜度），但当梁的长度较短时（Lb/Tb＜5时），装配力会很大且梁根部应变大，采用锥形梁（锥度比Tr/Tb在0.5~0.8之间），可以将应变均匀地分布在梁的各处，减小梁根部应力集中。

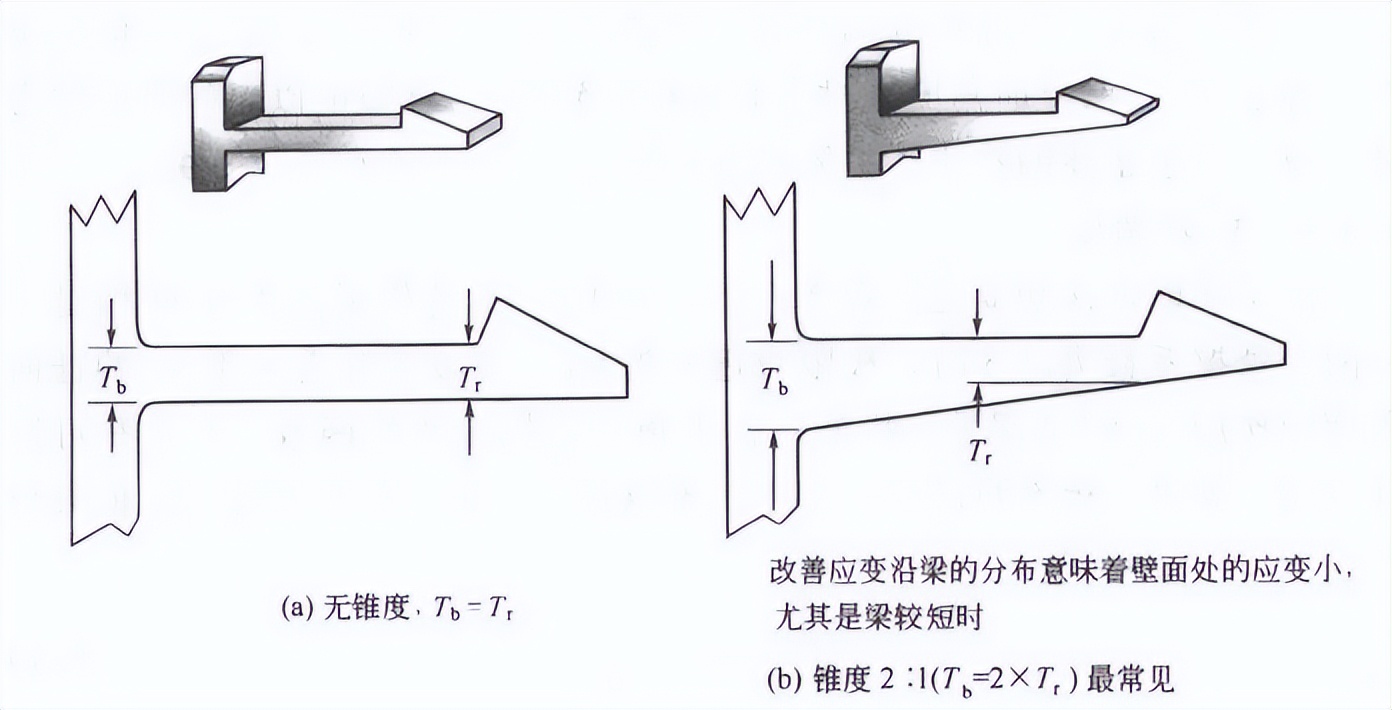
当Tr/Tb=0.5时，卡扣的综合性能较好。

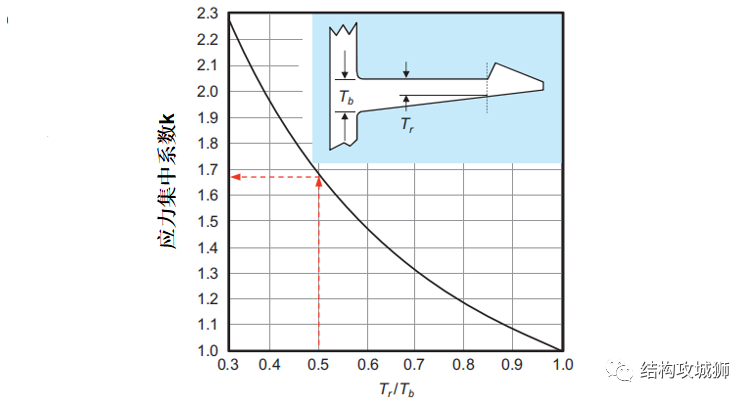
7、梁的宽度Wb

常见的卡扣，梁的宽度从根部到保持面变化不大，只有较小的出模斜度，此时梁的宽度不影响最大装配应变，但影响装配力、分离力和保持强度，当梁的宽度大于长度的1/2时，此时的悬臂梁不像梁而更像平板，应用梁理论计算时，误差较大。

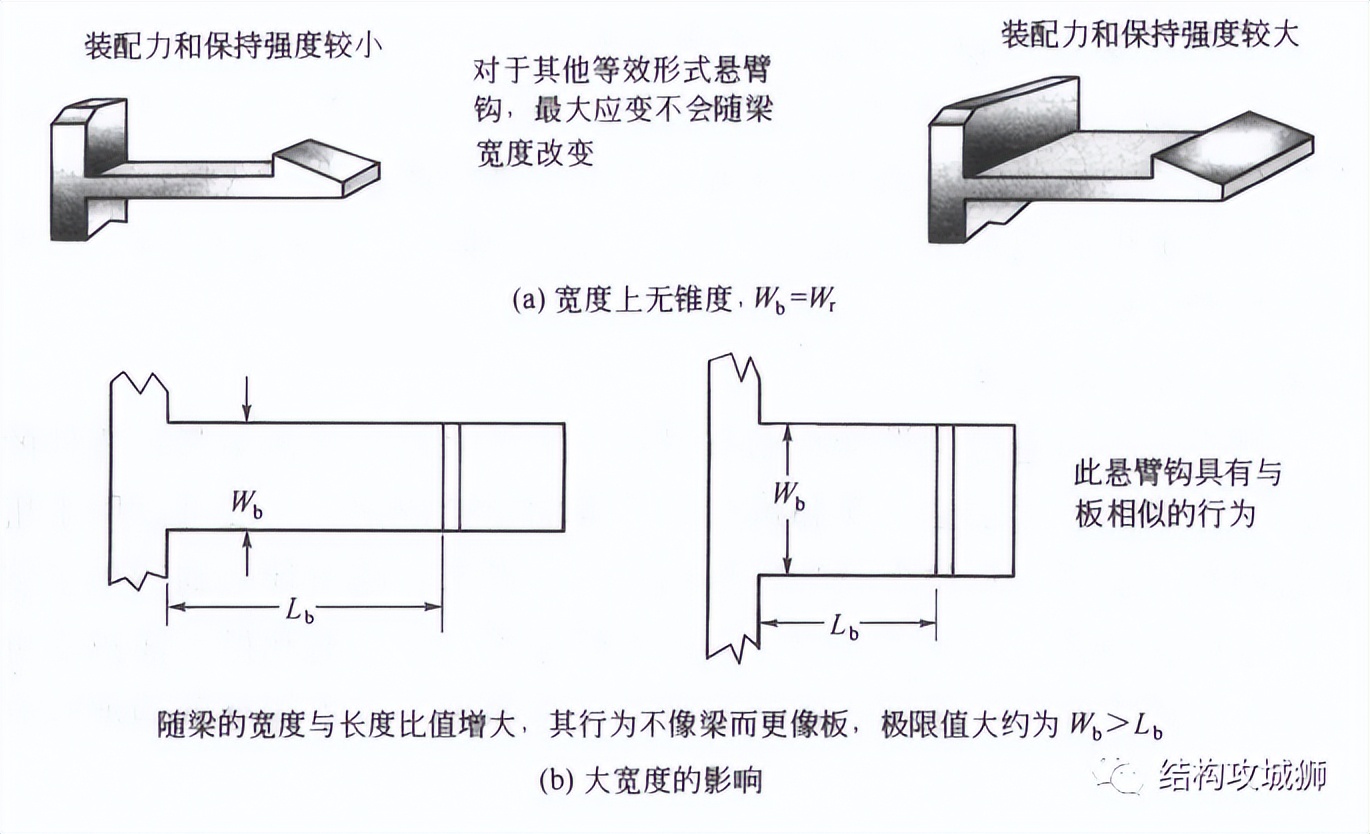
梁在宽度上也可以像梁厚度一样带锥度，宽度带锥度的梁可以减小梁根部的应变，但不如厚度带锥度那么有效。（梁的宽度带4:1锥度时，才能得到与梁厚度带2:1锥度时同样量级的应变减小效果）

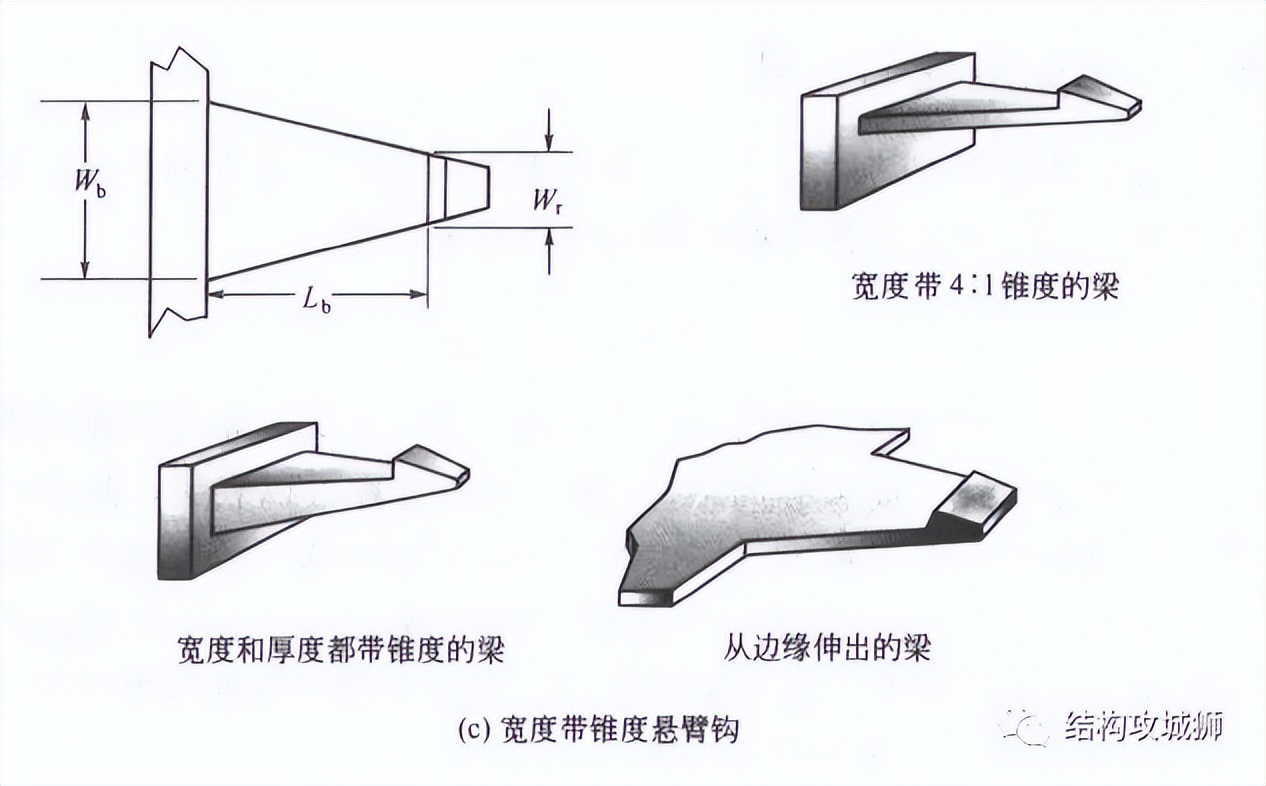
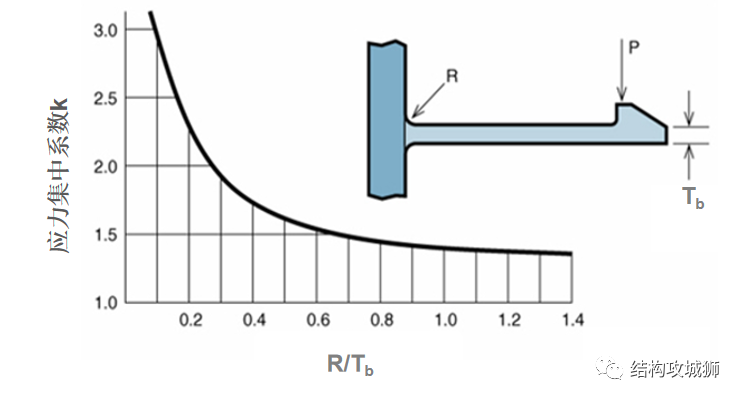
8、梁的根部半径R

应力集中会造成梁根部的实际应变增大，在梁的根部导R角可以减小应力集中，R的取值为梁宽度的50%时，综合性能较好。

二、悬臂梁卡扣的相关计算：

为了确保卡扣性能能够满足实际应用要求，需要进行详细计算分析和终端应用试验。一般计算偏斜力、装配力、分离力、最大变形量。以下以恒定矩形截面的悬臂梁卡扣为例介绍具体计算步骤。

在实际设计时，通过上述介绍，可以首先确定卡扣的以下尺寸参数。

1、梁根部初始应变的计算

由悬臂梁理论可推导出以下应变公式：

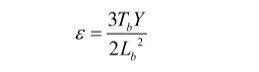
将计算结果与材料的最大许用应变相比较。

2、最大偏斜力的计算

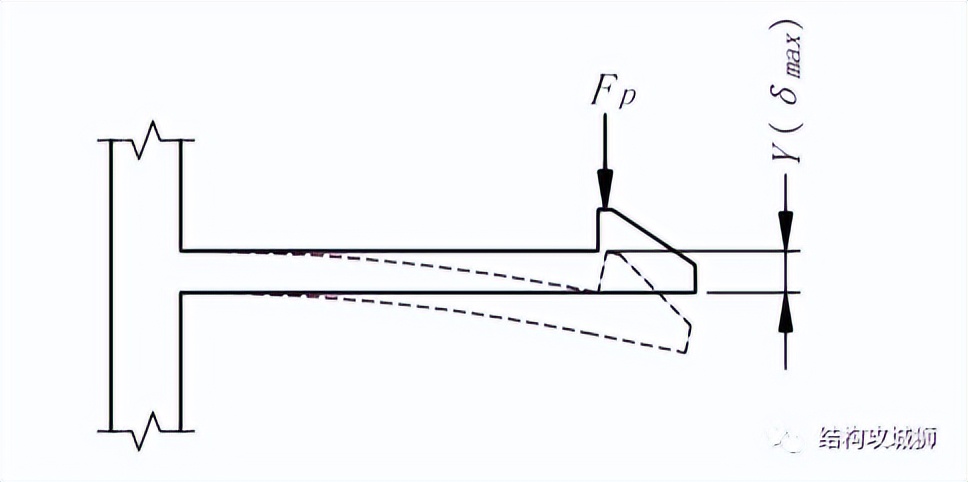
最大偏斜力（Fp）：使卡扣悬臂梁末端在许用应变内发生偏斜（δ）时所需要的力。一般情况下，悬臂梁最大量δmax就是卡扣保持面深度Y。

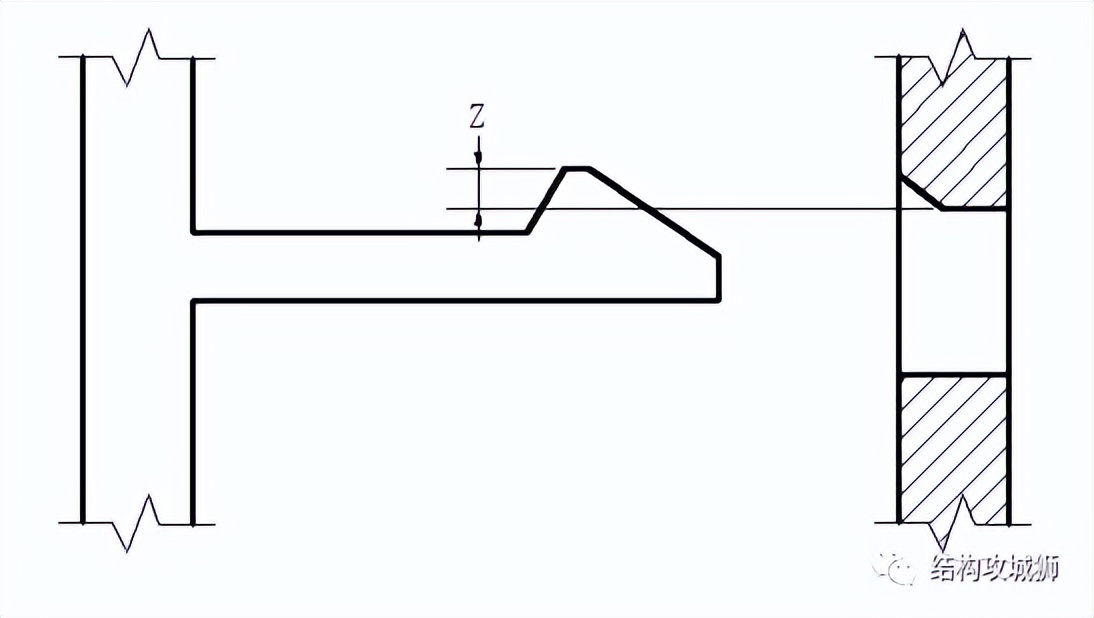
但，在实际产品结构设计中，我们更关心的是保持面与配合功能件之间的搭接量Z（卡合量），对于需拆卸的结构，搭接量Z需小于Y，越小越容易装配和拆卸，但保持强度越低，反之亦然。对于可拆卸无冲击、碰撞、跌落测试要求的产品结构，搭接量Z建议取值在0.3~0.6之间，反之，搭接量Z可设计在0.7~1.2之间，甚至更大。

同样由悬臂梁理论可推导出以下公式：

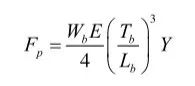
实际上，计算结果与实际相比会偏大，那是因为装配过程中，卡扣壁面的偏斜、配合功能件的偏斜都会对卡扣的性能有影响，当壁面偏斜时，梁的实际力、强度、应力、应变都比计算值小，当梁长度与厚度的比值越小时，偏斜的影响就越明显。

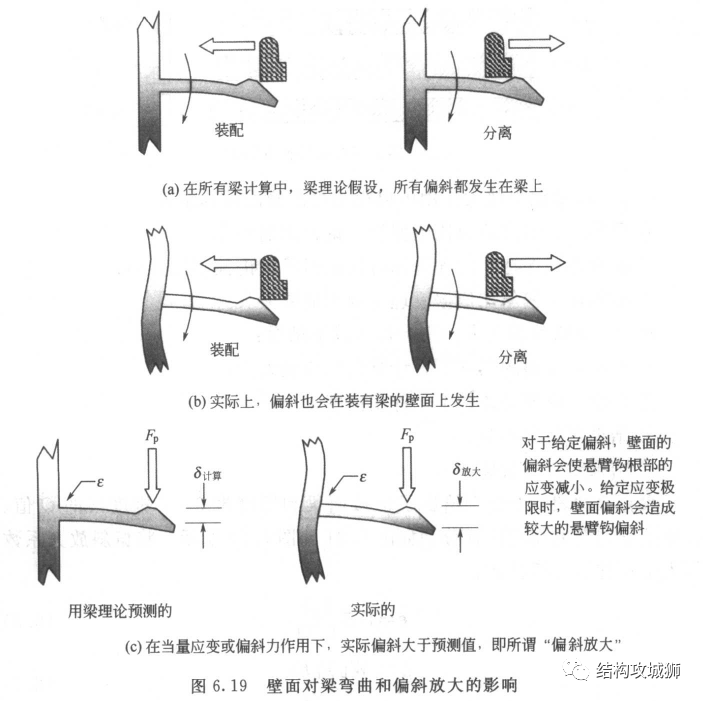
卡扣在不同壁面上对偏斜放大的影响是不同的，如下图。

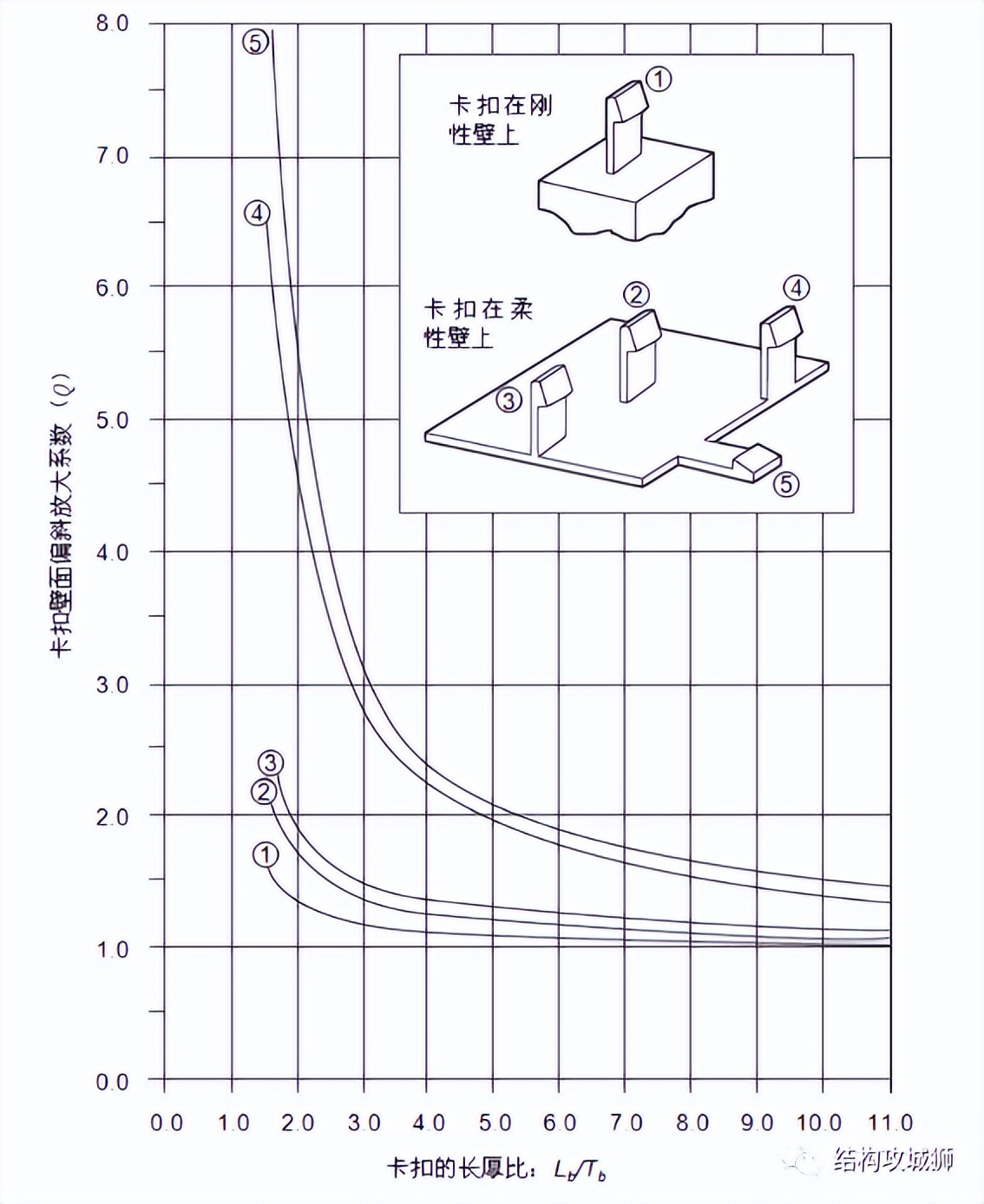
同样，在装配的过程中，配合功能件也可能发生偏斜，如果偏斜明显的话，对计算结果也会产生影响，主要影响装配力、拆卸力、保持强度和应变。

因此，需要对以上初始应变、偏斜力进行修正，引入壁面偏斜放大系数Q、配合功能件放大系数K，如下：

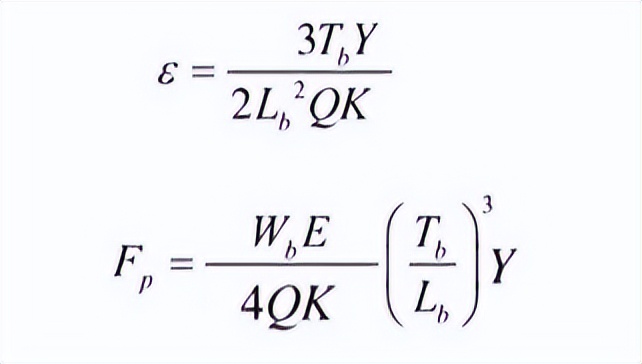
此时，通过以上公式，也可以计算出在一定偏斜力Fp的作用下，卡扣末端最大变形量Y。

3、装配力的计算

由于悬臂卡扣的特性，卡扣在装配的过程中悬臂梁会发生偏斜，插入面角度会跟随变化，装配力也发生变化，很显然，最大插入面角度出现在悬臂梁偏斜最大时，因此，为了计算最大装配力，必须先确定偏斜最大时的角度。

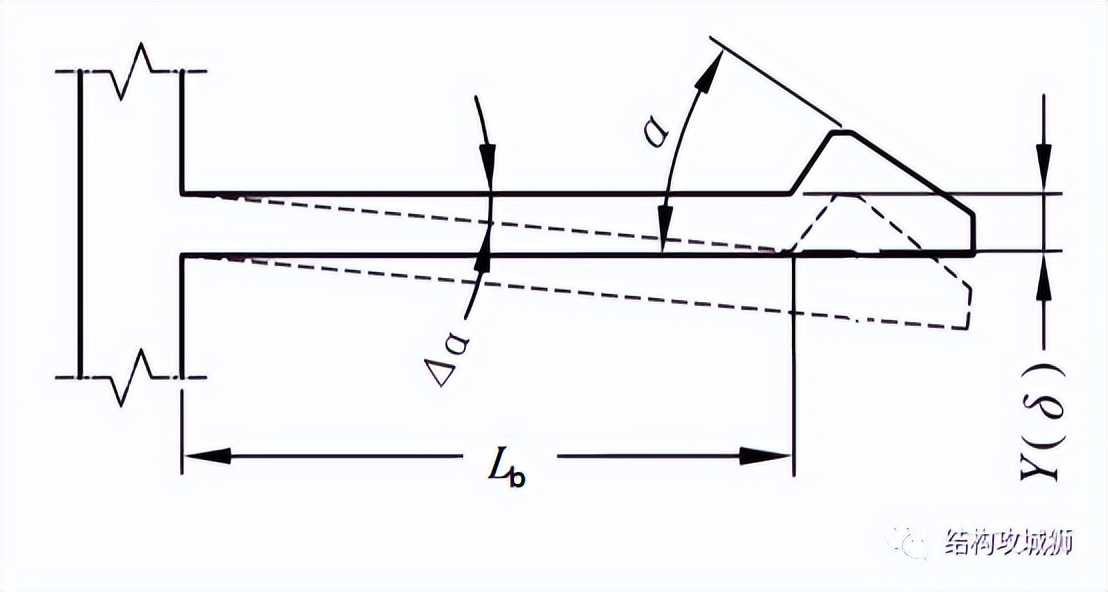
插入面角度变化的简化公式为：

受力分析：

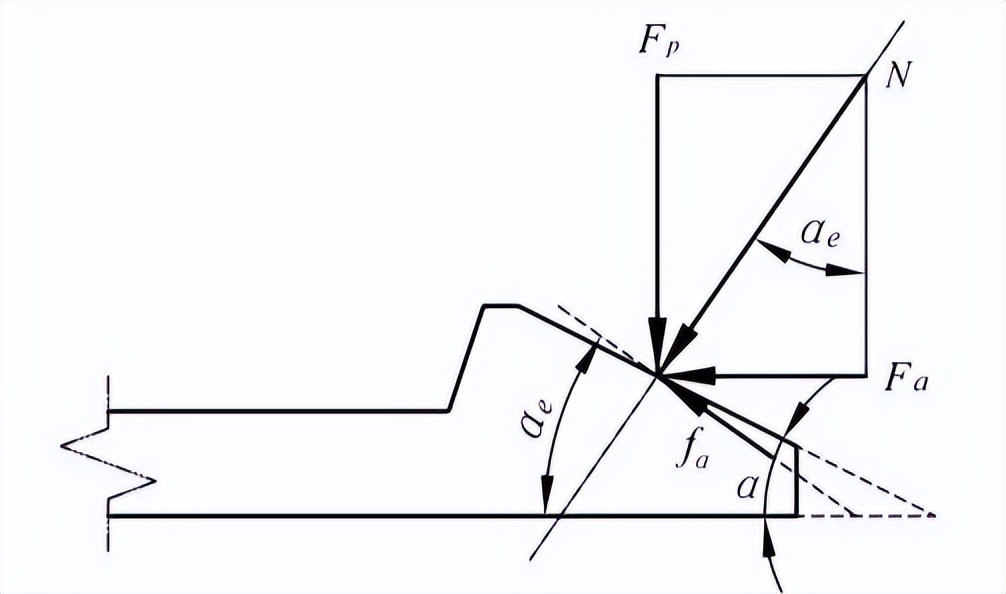
由以上受力分析图可列出力平衡方程：

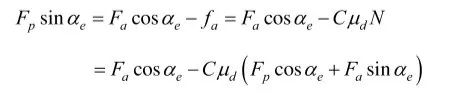
4、分离力、保持力的计算

卡扣在脱开的情况有两种，一种是有意的，即人为分离卡扣零件所需要的力，叫做分离力；另外一种是无意的，即锁紧件抵抗无意脱开的力，叫做保持力。

所以，如果我们关心的是分离（可拆卸卡扣）的难易程度，则要计算最大分离力；如果我们关心的是保持强度，即保持力，则要计算最小分离力。

实际上这两种力区别不大，只是在保持面角度因悬臂卡扣中的剩余偏斜存在时（卡扣装配后，由于误差原因，悬臂梁无法回复到原位而存在一个偏斜角度），需要计算实际角度。

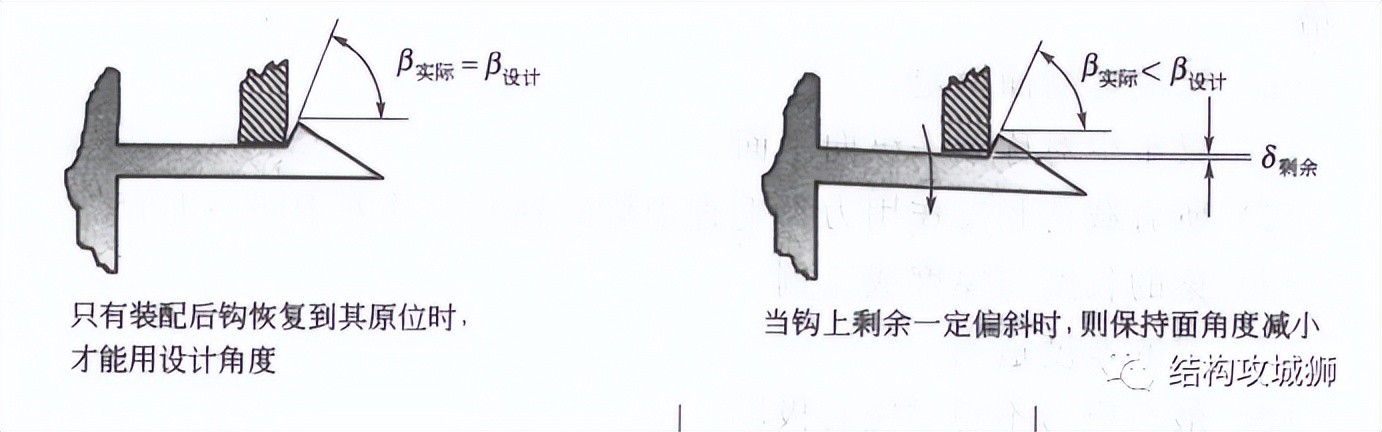
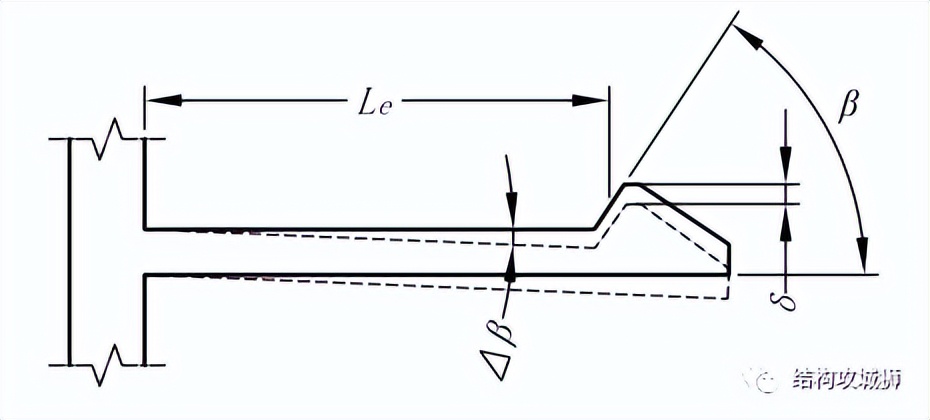
保持面角度计算方法与插入面类似：

受力分析：

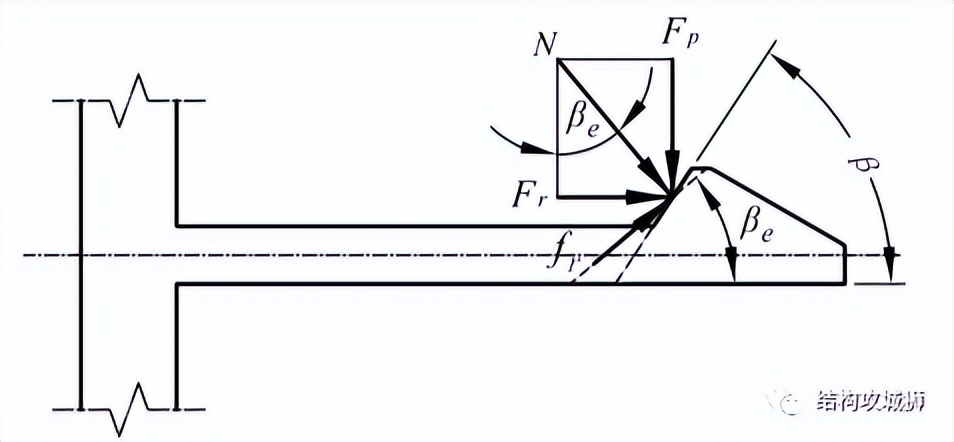
由以上受力分析可列出力平衡方程：

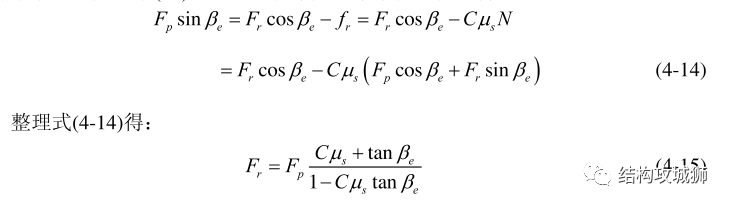
在实际结构设计中，卡扣悬臂梁与配合功能件之间一般留有间隙，故一般不存在剩余偏斜，计算时可直接用设计的保持面角度β。

举例：

有如下卡扣，Tb=1，Lb=7，Wb=5，Y=1，α=30°，β=50°，材料为ABS，求装配力和保持力。

通过查资料可知，弹性模量E=2100Mpa，摩擦系数μ=0.5，εmax=2.5%，由于Lb/Tb=7，查表，取偏斜放大系数Q=1.13，配合功能件放大系数K=1.25，把上述值代入以下公式：

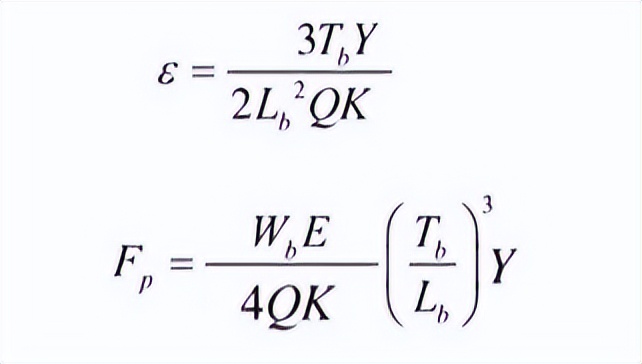
可得， ε=2.17%<εmax，满足要求；Fp=5.4N；

计算插入面有效角度：

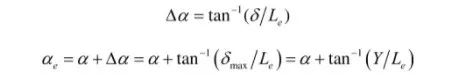
代入计算得，αe=38°；

代入计算得，Fa≈14N，（同种材料，C取1.2）

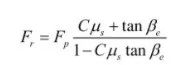
代入计算得，Fr≈34N；

所以装配力为14N，保持力为34N。

本篇介绍到此，以上大部分内容其实参考以下文献，如读者遇到不是很清楚地方，建议去看看原文献，里面会讲得比较清楚。

参考文献：

1. 著：保罗 R.博登伯杰，译：冯连勋、冯秀青、董力群、梁军，塑料卡扣连接技术。

2. 林杨明，塑料制品悬臂卡扣连接件设计方法的研究。

免责声明：

本文来源于结构攻城狮，出于对原创的保护，转载的文章我们一般给与标注来源，转载目的是在于传递更多信息，并不代表本号赞同其观点和对其真实性负责。如涉及作品内容、版权和其它问题，请及时与我们联系，我们将在第一时间删除内容。