舍弗勒于2018年推出其高速同轴电桥(最高转速18000rpm),搭载于奥迪e-tron车上。该电桥采用高速行星轮系,结构紧凑,轻量化(齿轮箱仅16kg),高功率密度,高扭矩密度。目前拆解报告多见诸于某些自媒体或公众号,但未见详细的解析。本文试从传统差速器入手,简析舍弗勒同轴电桥工作原理。
01 传统差速器工作原理
差速器的本质是将输入动力平均分配给左右半轴,同时允许左右半轴转速不同。传统直齿伞齿轮差速器的工作原理在很多教科书上都有详细论述,在此不在赘述,本文从行星排的角度结合模拟杠杆建立传统差速器运动学和动力学方程,以方便下文讨论舍弗勒同轴电桥。
传统差速器的结构简图如图1所示
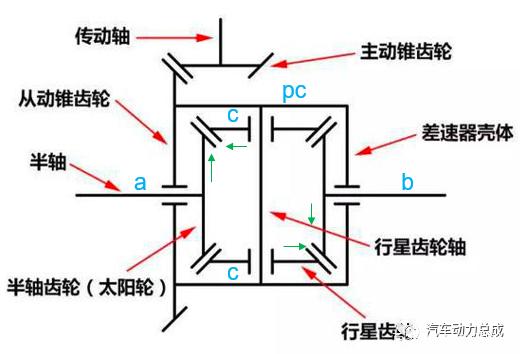
图1 差速器结构简图(图片来源于网络)
根据图1,用相对速度法(见机械原理教材)使得行星架PC的转速为0,即PC固定,则整个差速器为定轴传动。图1中绿色箭头表示在定轴传动情况下半轴齿轮和行星齿轮的旋转方向,据此建立模拟杠杆图如图2,两个半轴在行星架的两边(转速相反)。
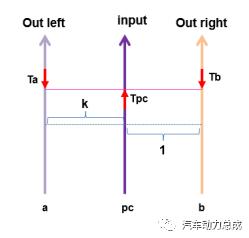
图2 传统差速器模拟杠杆图
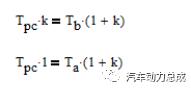
所以
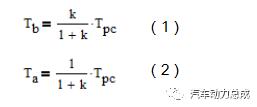
若要满足动力均分原则,则上式(1)和(2)必然相等,即特性参数k=1,将k值代入式(1)、(2)得
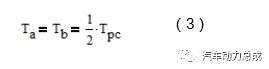
进一步的,根据图1,当行星架固定时,两半轴的转速比
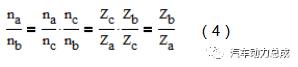
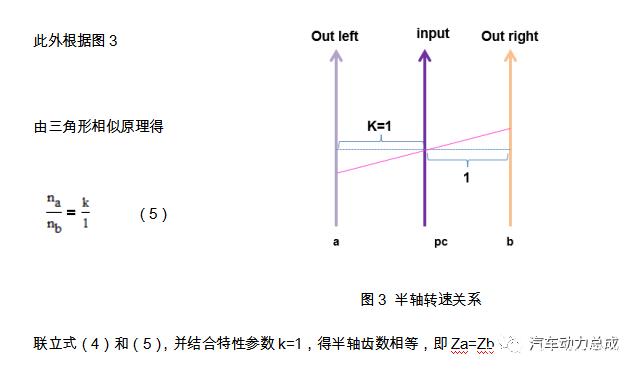
02 舍弗勒同轴电桥
2.1 舍弗勒同轴电桥结构

图4
舍弗勒同轴电桥是NW行星排和不带齿圈的拉维纳行星排的组合,两个行星排共用行星架,NW行星排相当于二级减速齿轮,实现电机的降速增扭,拉维纳行星排通过特殊配齿使得两太阳轮齿数相等,从而实现均分输入动力的功能。
2.2 NW行星排分析
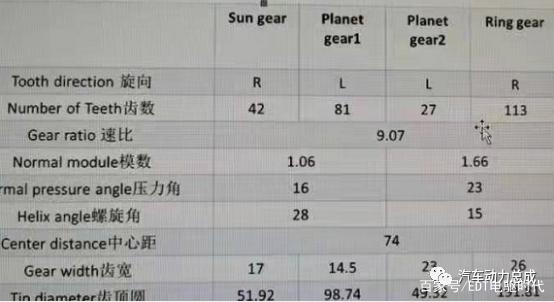
舍弗勒同轴电桥的NW行星排的齿轮参数如下表
表1 NW行星排齿轮参数
其结构简图和模拟杠杆如下图
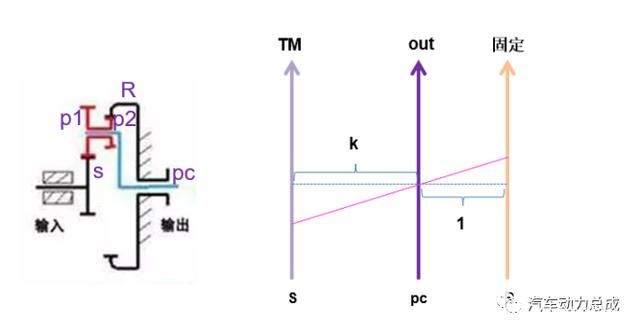
图5
仿上一节讨论,当行星架固定时求解特性参数如下
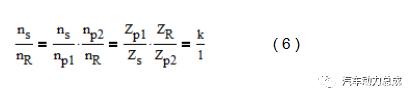
将表1中的齿数代入式(6)得特性参数k=8.07
传动比求解如下图,当齿圈固定,太阳轮连接驱动电机作为动力输入,行星架输出时,其减速比
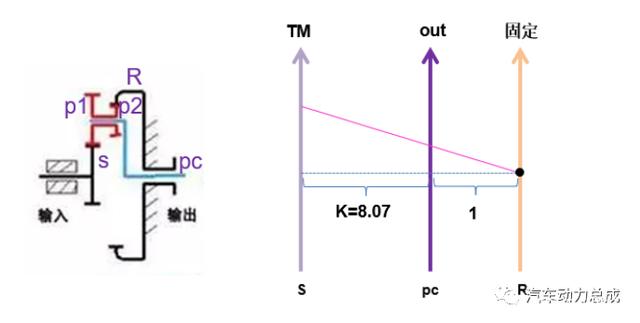
图6
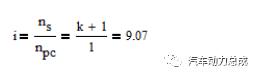
2.3 轻量化差速器分析
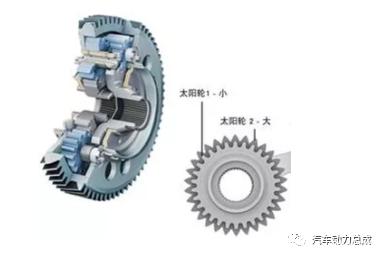
图7
舍弗勒轻量化差速器正是运用了上一节中分析的输入动力均分原理,某种机构只要能够将输入动力平均分配给左右半轴,并允许左右半轴的转速在一定范围内波动即可作为差速器使用。要分析该机构,首先还是建立模拟杠杆图,并求出行星排特性参数。
该机构为无齿圈拉维纳行星排,其模拟杠杆如下图
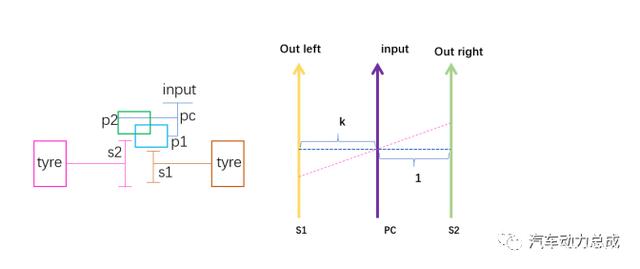
图8
上图中,当行星架固定时,左图为定轴传动,则
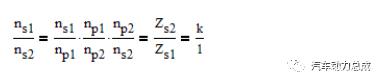
图7右侧中两太阳轮齿数为30,代入上式得k=1,这跟第一节中所述的传统差速器特性参数一致,下面证明其输入扭矩的均分。
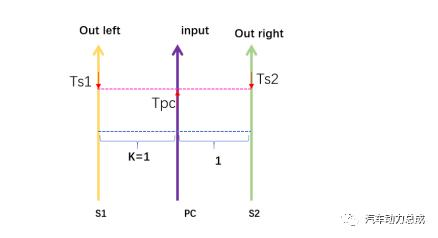
图9
在图9所示的杠杆图中,分别对s1和s2轴取矩,根据杠杆平衡,有

该式即表明,行星架上的输入扭矩平均分配到左右半轴上,满足了该机构可以作为差速器使用的充分条件,而必要条件即为两半轴(太阳轮)同时和行星轮啮合,允许转速不同时其转速差由行星轮自转来补偿。
2.4 同轴电桥的动力流向
将2.2节和2.3节描述的行星排组合在一起即为舍弗勒AKA320同轴电桥,如图10
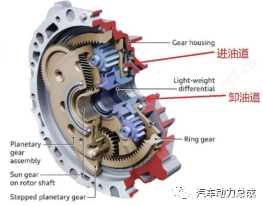
图10
其动力走向在图11所示的结构简图上表示
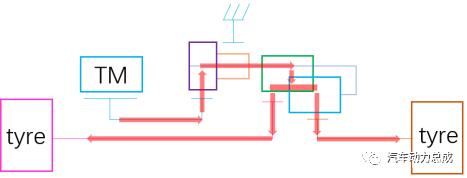
03 总结
差速器的本质是将输入动力均分给两个半轴,并允许两半轴存在转速差。从模拟杠杆的角度看传统直伞齿轮行星排差速器的特性参数是1,此外不带齿圈的拉维纳行星排经过合理配齿也可以实现特性参数是1(舍弗勒AKA320)。这类构型虽然解决了动力均分的问题但是正是由于杠杆比是1,所以没法降速增扭,必须增加减速机构。目前的解决方案有三种,一般的方案是两级减速+传统差速器,这种方案也是目前主流的解决方法;此外有行星排+传统差速器,比如美桥、加特克等就是行星排实现减速增扭,传统差速器实现动力均分;除此之外就是行星排+行星排的方案,如本文所述舍弗勒的后减速器同轴式电桥。两级减速的方案属于平行轴,需要的空间较大、笨重,如果追求轻量化、高效率、高功率密度,那就需要同轴的打法。


 加载中,请稍侯......
加载中,请稍侯......